In the previous article we’ve implemented the major scales, and caught a bug.

In this article we’re going to fix the bug by testing our command line tool and we’re going to rethink our data model.

Music theory-wise we’ll briefly cover flat notes and naturals.

After everything works correctly, you’ll see how easy it is to add features. Then we are going to give our program a test-run by combining programs on the command line.

Every letter must appear once

Last time we ended up with a working program that gives us major scales, such as the C and G scale:

% swift run music --scale c
C D E F G A B

% swift run music --scale g
G A B C D E F♯

But our program has a bug. Let’s try the F scale:

% swift run music --scale f
F G A A♯ C D E

Uh oh, music theory states that every letter must appear in a scale exactly once. Instead, we have two A notes (even though one is sharp), and there is no B!

Our program is technically correct though. The F scale does follow the major scale, namely: whole whole half, whole whole whole half steps.

As programmers we can say “works on my machine” and call it a day. But musicians are a bit more picky about this. They really need to see each letter only once.

So how do we solve our scale problem? By introducing another accidental.

Introducing ♭

Last time, we’ve seen that if we grab a note, like C, we can raise it a half step, and make it a C-sharp, written as C♯. The ♯ is called an accidental.

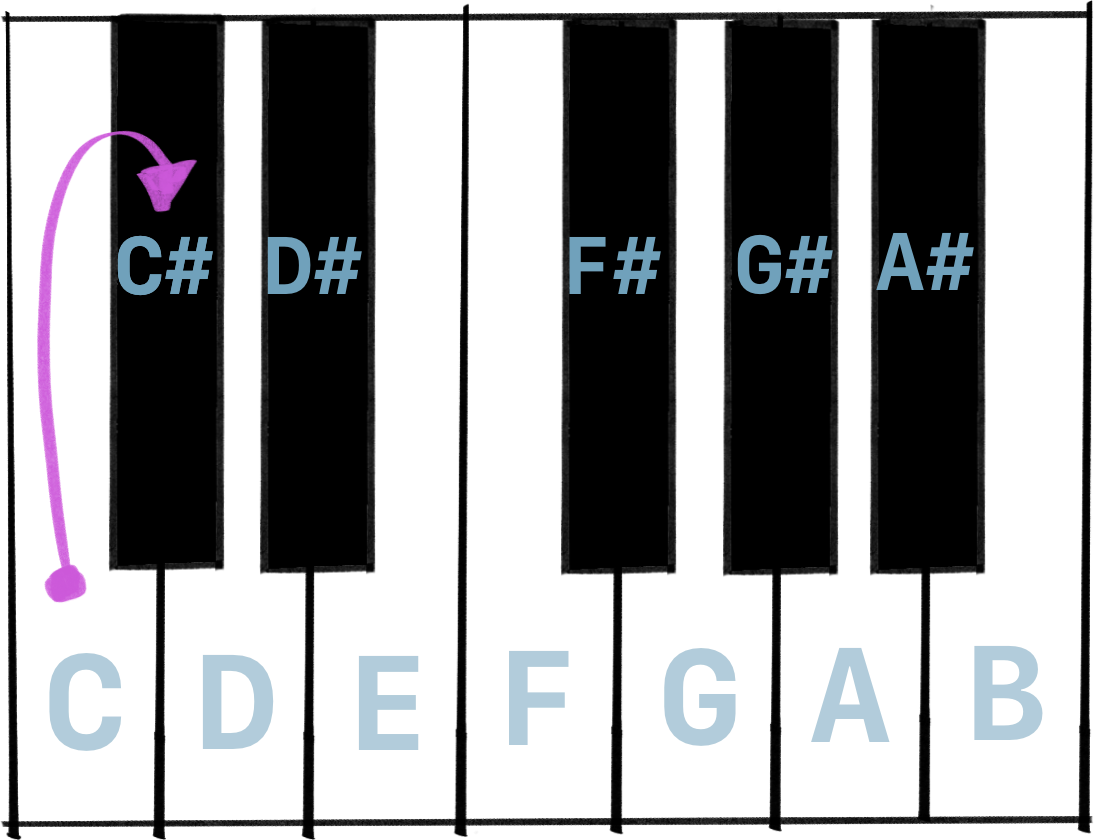
We can do the opposite by lowering a note by a half step. Say hello to our new friend ♭, pronounced flat.

Now if we take a D note, and we flatten it, we get D♭ (pronounced D-flat).

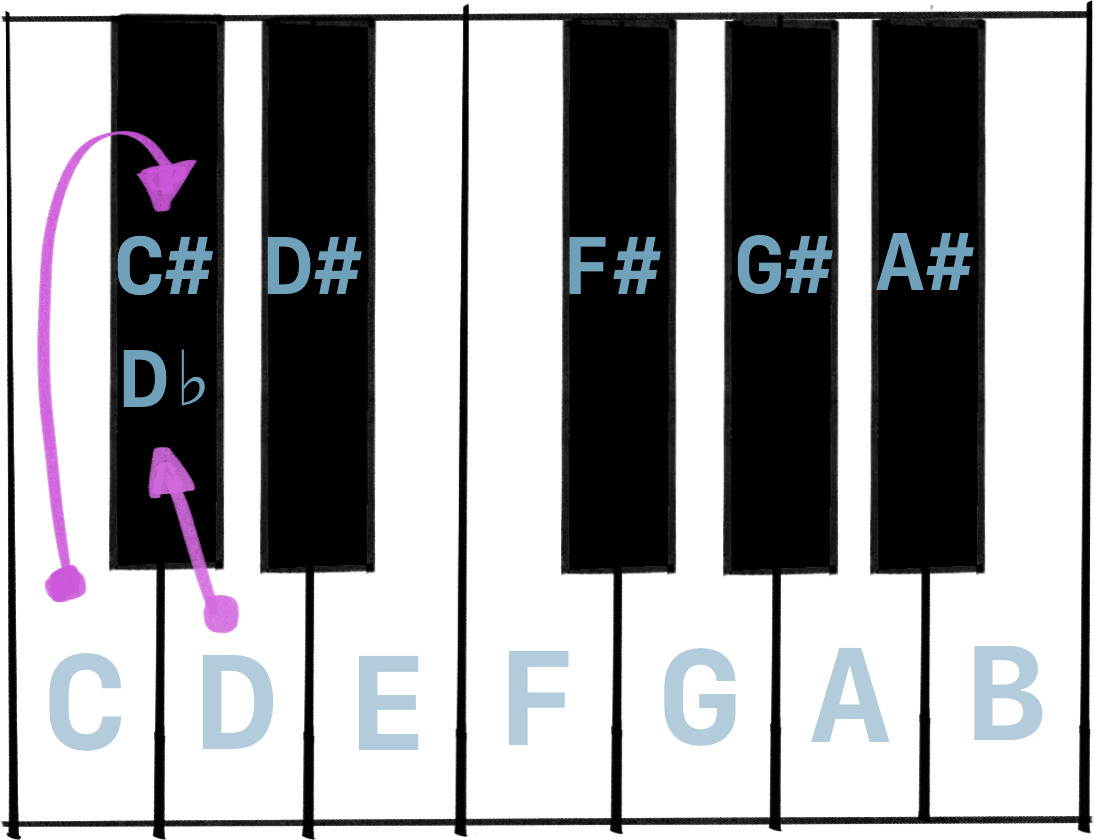
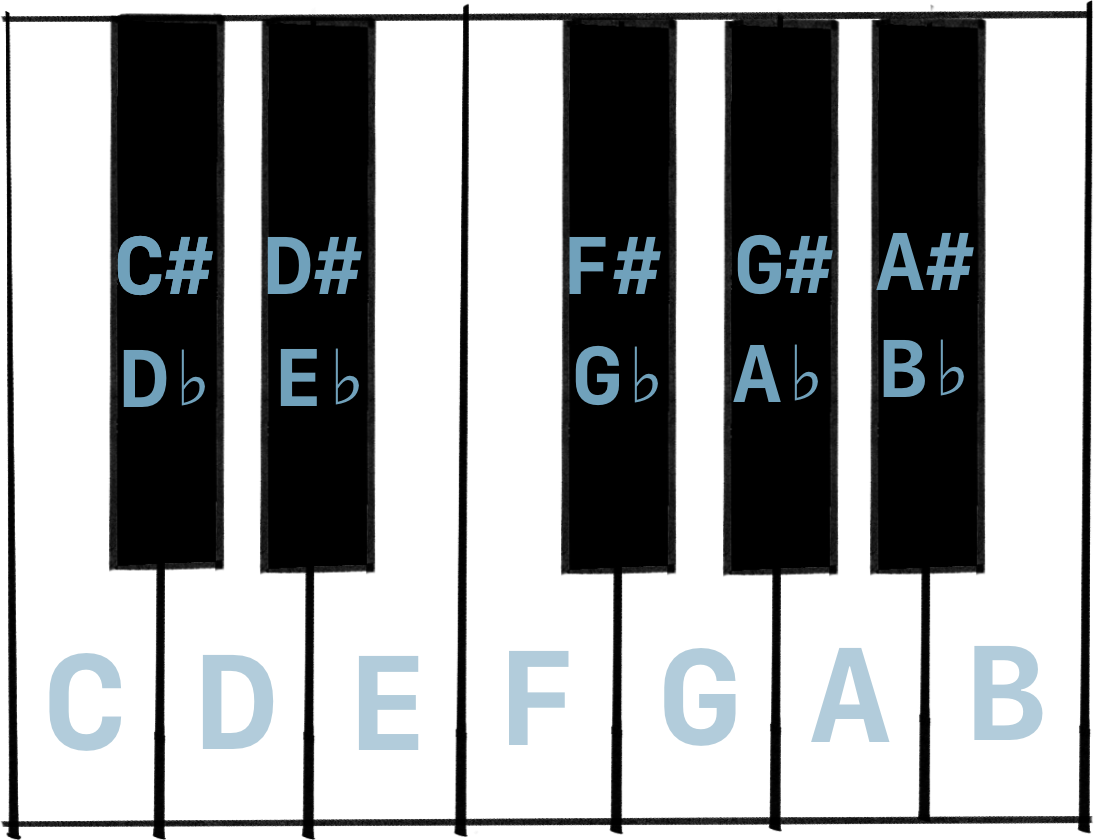
This means that accidentals can have multiple names. Notice how C♯ and D♭ are the same note!

Should we call it a C♯ or D♭ ? It depends on the context. And in order to fix our scales, we will make sure to use each letter once, and flatten or raise accordingly.

Let’s add the missing flats so we get acquainted. Then we’ll start implementing it.

Writing out an algorithm

Before we just start coding and updating our algorithm, it’s a good idea to write it out first; This helps us reason about what we’re trying to do. Writing it out is a helpful technique to solve (programming) puzzles.

Let’s make the F scale again. This time, let’s start without accidentals and make sure all letters appear only once.

F G A B C D E

That’s a good start. Now we’ll apply the major scale again. First a whole step. So after F comes G. No accidentals needed.

F G A B C D E
  ^

Then another whole step after G, we reach A. Again, no accidentals are needed.

F G A B C D E
    ^

Now we perform a half step. A half step after A is A♯ which our program incorrectly outputs. It is technically correct but still faulty, because it would violate the “letters appear only once”-rule.

This time we have to do something with a B. The solution? We can flatten B to a B♭ to reach the half step.

F G A B♭ C D E
      ^

Next, a whole step again from B♭. We end up at C.

F G A B♭ C D E
         ^

Another whole step, we reach D.

F G A B♭ C D E
           ^

Another whole step, we reach E.

F G A B♭ C D E
             ^

Great, so the F major scale is F G A B♭ C D E. Every letter appears only once, musicians will be happy.

Adding tests

Now that we know how to fix our scales, let’s prepare some tests so that they will fail on purpose. After that, we’ll refactor our code to make all tests pass.

We’ve learned about the C, G, and F major scales. Let’s define those as expectations by making an array of pairs. The first element in the pair is the scale we want, the second element is an array of the expected notes.

Then we call our custom runWithArguments(args:string) method to run the tests against the command line tool. This method contains a lot of boilerplate that’s generated for us. I modified it a little so we can pass an argument string.

import XCTest
import class Foundation.Bundle
import music // Notice how we don't use @testable import?

final class musicTests: XCTestCase {

    func testMajorScales() throws {
        let expectedPairs = [
            ("a", "A B C♯ D E F♯ G♯"),
            ("b", "B C♯ D♯ E F♯ G♯ A♯"),
            ("f", "F G A B♭ C D E"),
        ]

        for (note, expectedScale) in expectedPairs {
            let output = try runWithArguments(args: "--scale \(note)")
            XCTAssertEqual(expectedScale, output, "Scale of \(note) is incorrect")
        }
    }

    private func runWithArguments(args: String) throws -> String {
      // ... snip
    }
}

If you want to see the full runWithArguments method, you can check it out on github. I left it out because it’s 90% boilerplate, generated by the Swift Package Manager.

Adding variants to our tests

As a bonus, we can make sure our program is a bit more robust. Not only will we accept lowercased notes / scales as input. We can add more variants. For example, we’ll also verify that uppercase letters work properly. This will make our program more robust.

Let’s grab expectedPairs, and double them, one with a lowercase and one with an uppercase note/scale.

In other words, a list like the following…

[("c", "C D E F G A B"),
 ("g", "G A B C D E F♯"),
 ("f", "F G A B♭ C D E")]

…becomes:

[("c", "C D E F G A B"),
 ("C", "C D E F G A B"),
 ("g", "G A B C D E F♯")
 ("G", "G A B C D E F♯"),
 ("f", "F G A B♭ C D E"),
 ("F", "F G A B♭ C D E")]

Naively, we can use map and return both variations…

let variants = expectedPairs.map { note, expectation in
    [(note.lowercased(), expectation), (note.uppercased(), expectation)]
}

… but then we’ll end up with a nested array.

Instead, we can use flatMap to flatten the nested array again after mapping. In fact, if it was called mapFlat, it would tell us more about the order of the operations. First it maps, then it flattens.

We only rename map to flatMap, the closure stays the same. This will flatten the nested array one layer.

let variants = expectedPairs.flatMap { note, expectation in
    [(note.lowercased(), expectation), (note.uppercased(), expectation)]
}

As an improvement to make our program more robust, we can generate more variants besides uppercase and lowercase, such as accepting the ♯ and ♭ characters, but I think we’re good for now.

Adding more scales

To save some time, I also added a few other scales. Our final test looks as follows:

import XCTest
import class Foundation.Bundle
import music

final class musicTests: XCTestCase {

    func testMajorScales() throws {
        // We're expanding expectedpPairs
        let expectedPairs = [
            ("a", "A B C♯ D E F♯ G♯"),
            ("b", "B C♯ D♯ E F♯ G♯ A♯"),
            ("c", "C D E F G A B"),
            ("d", "D E F♯ G A B C♯"),
            ("e", "E F♯ G♯ A B C♯ D♯"),
            ("f", "F G A B♭ C D E"),
            ("g", "G A B C D E F♯"),
        ]

        let variants = expectedPairs.flatMap { note, expectation in
            [(note.lowercased(), expectation), (note.uppercased(), expectation)]
        }

        for (note, expectedScale) in variants {
            let output = try runWithArguments(args: "--scale \(note)")
            XCTAssertEqual(expectedScale, output, "Scale of \(note) is incorrect")
        }
    }

    private func runWithArguments(args: String) throws -> String {
      // ... snip
    }
}

Refactoring notesIn(scale:)

We know how to fix the scales, and our tests will make sure we are doing it properly. Let’s refactor our notesIn(scale:) method now to make all tests pass.

We’ll use the wishful thinking method again — as covered in the previous article — where we write out our code and pretend everything exists. Then after we’re done, it will compile and we will be completely done.

To get a scale, our approach is now different. Last time we iterated the steps and grabbed each note depending on the size of the step.

This time, we’re going to make sure we have all letters. For example, for a scale of F we make sure to start with F G A B C D E. We do this by asking for a notes’ naturals. A natural is a regular note without any sharps or flats.

Then we iterate over all notes and augment them if necessary. The new augment function will either sharpen or flatten a note, or leave the note as is (natural). Thanks to wishful thinking, we don’t have to think about how augment will work, this way we can focus on notesIn(scale:) first.

/// Get the notes from a major scale.
/// - Parameter scale: A scale
/// - Returns: An array of notes folliowing a major scale pattern
func notesIn(scale: Scale) -> [Note] {
    // We grab major the pattern.
    let majorScalePattern: [Step] = [.whole, .whole, .half, .whole, .whole, .whole, .half]
    // We grab all regular notes (no sharps or flats).
    // Then we rotate them.
    // The scale that's passed will be turned natural to make `rotated` work.
    // We can't rotate naturals to B♭, for example.
    let notes = Note.naturals.rotated(to: scale.natural)

    // We prepare for iteration.
    // The scale note is the first note, no augmentations.
    var previousNote: Note = scale
    // We are collecting augmented notes
    var augmentedNotes = [previousNote]
    for (note, step) in zip(notes.dropFirst(), majorScalePattern) {
        // We augment a note, such as turning C into C♯, or B into B♭.
        let augmentedNote = augment(previousNote: previousNote, note: note, step: step)
        // We save the new note.
        augmentedNotes.append(augmentedNote)
        // We update the last iterated note
        previousNote = augmentedNote
    }

    // We return all augmented notes
    return augmentedNotes
}

Our code won’t compile yet. (That’s the wishful thinking method).

Writing it out means a couple of things:

First, we need a naturals property on Note, because we don’t want any sharps or flats.

Second, we need some kind of augment function. Let’s start with that because we may need more Note modifications.

Now that notesIn(scale:) is ready, we can zoom in and focus on augment(previousNote:note:step:).

Implementing the augment function

To make augment work, we need a note and a step. But we also need to know how far it’s removed from the previous note.

There are many approaches we can take. The one I chose is to give numerical values to accidentals. We’ll make flats a –1, regular — or natural — notes a 0, and sharps are +1.

For example, G♭ is –1, G is 0, and G♯ is 1.

Then a half step is +1, and a whole step is +2.

So if previousNote is a G and the current note we have to augment is an A, then adding +1 (half step) would make it an A♭, and +2 (whole step) would make it an A.

Then one more pesky thing remains. There is no step between B and C, and between E and F. We need to account for that edge-case by adding an extra step to the total in these cases.

Depending on the total value, we can decide to sharpen or flatten a note, or leave it as is.

/// augment makes a note sharp, flat, or natural
func augment(previousNote: Note, note: Note, step: Step) -> Note {
  let missesAccidental = previousNote.name == .b || previousNote.name == .e
  let halfStepValue = missesAccidental ? 1 : 0
  let stepValue = step == .whole ? 2 : 1

  let totalValue = previousNote.value + stepValue + halfStepValue

  switch totalValue {
  case 1: return note.flatten()
  case 2: return note.natural
  case 3: return note.sharpen()
  default:
    fatalError("Unsupported \(totalValue)")
  }
}

Nesting a function

The final notesIn(scale:) function will look as follows.

Notice that I made augment(previousNote:note:step:) a nested function. I know that this is a bit controversial, but I like it a lot.

Here’s why: Nothing in the entire codebase needs the augment function. It’s local to our code. It’s more private than a private function. It’s right there where you need it, no need to scroll to a deeply hidden function, and nobody else can access it, so its intent is quite clear and it doesn’t clutter the namespace. Over time, I’ve really gone to appreciate them.

If you have different style preferences, then feel free to place it in a different namespace of course.

/// Get the notes from a major scale.
/// - Parameter scale: A scale
/// - Returns: An array of notes folliowing a major scale pattern
func notesIn(scale: Scale) -> [Note] {
    func augment(previousNote: Note, note: Note, step: Step) -> Note {
        let missesAccidental = previousNote.name == .b || previousNote.name == .e
        let halfStepValue = missesAccidental ? 1 : 0
        let stepValue = step == .whole ? 2 : 1

        let totalValue = previousNote.value + stepValue + halfStepValue

        switch totalValue {
        case 1: return note.flatten()
        case 2: return note.natural
        case 3: return note.sharpen()
        default:
            fatalError("Unsupported \(totalValue)")
        }
    }

    let majorScalePattern: [Step] = [.whole, .whole, .half, .whole, .whole, .whole, .half]
    let notes = Note.naturals.rotated(to: scale.natural)

    var previousNote: Note = scale
    var augmentedNotes = [previousNote]
    for (note, step) in zip(notes.dropFirst(), majorScalePattern) {
        let augmentedNote = augment(previousNote: previousNote, note: note, step: step)
        augmentedNotes.append(augmentedNote)
        previousNote = augmentedNote
    }

    return augmentedNotes
}

Let’s recap where we are and what we need to do.

• We need to be able to turn a note into a value (–1, 0, or 1).
• We also learn that note needs a few more methods and properties. Namely flatten(), natural, and sharpen(), on top of the new naturals property.

Let’s update Note now to make our code compile. After everything compiles, we should have a working program!

Refactoring Note

Last time, we modeled Note as an enum with regular notes and sharps.

enum Note: String, Equatable, CaseIterable {
    case a, aSharp
    case b
    case c, cSharp
    case d, dSharp
    case e
    case f, fSharp
    case g, gSharp

    // .. snip
}

Using an enum is now going to be problematic.

Let’s say we want to implement flatten(). We need to switch over all the notes and give their flat representation. Then we want to implement sharpen() to make a note a sharp, we again need to switch over all the notes and give their sharp representation. Now we want to make a note natural (no accidentals), and once again, we need to switch over all the notes.

You see where I am going with this? Every tiny change causes a lot of switch cases. And this is without adding the flats. We’d have dozens of cases each time. It’s not very ergonomical and causes a lot of boilerplate.

To make Note more ergonomical, let’s reconsider making it a struct. We will still have the same data, just shuffled around.

Modeling structs and enums

What do we need to make all the notes? The names of the notes for starters. So let’s make a Name enum containing the note names. We’ll use an enum here because each name is mutually exclusive. There is only one A, one B, one C, etc.

What else do we need? Accidentals, right? So let’s introduce a new Accidental enum with the three accidentals that we need to support.

We make sure to make Name of type String so that we can parse it more easily later. And we’ll implement CustomStringConvertible on Accidental.

Let’s convert Note to a struct which contains a name and accidental.

/// A representation of a musical note
struct Note: Equatable {

    enum Name: String, CaseIterable {
        case a, b, c, d, e, f, g
    }

    enum Accidental: CustomStringConvertible {
        case sharp
        case flat
        case natural

        var description: String {
            switch self {
            case .sharp: return "♯"
            case .flat: return "♭"
            case .natural: return ""
            }
        }
    }

    let name: Name
    let accidental: Accidental

}

Once we have a note, it will be very easy to augment it. We only need to switch over the accidentals, not all notes. We end up with significantly less boilerplate this way.

Below you can see the implementations for modifying all notes.

/// A representation of a musical note
struct Note: Equatable {
    // ... snip

    func flatten() -> Note {
        switch accidental {
        case .sharp:
            return Note(name: name, accidental: .natural)
        case .flat:
            fatalError("No support for double flat")
        case .natural:
            return Note(name: name, accidental: .flat)
        }
    }

    func sharpen() -> Note {
        switch accidental {
        case .sharp:
            fatalError("No support for double sharp")
        case .flat:
            return Note(name: name, accidental: .natural)
        case .natural:
            return Note(name: name, accidental: .sharp)
        }
    }

    var natural: Note {
        return Note(name: name, accidental: .natural)
    }
}

With relatively little code, we can now sharpen a note, flatten a note, or make it a natural.

Convenience methods

There is a downside. We can’t as easily refer to notes such as Note.a or Note.bSharp. But we might not need it anyway.

For convenience, we can add a initializer so we don’t always need to pass an accidental, a Note will by default by natural. We use an extension so that we can keep the so-called memberwise initializers that are generated for us.

Then we can add the naturals property by iterating over all the names and instantiating Note using this new initializer. This property is used in notesIn(scale:).

extension Note {

    init(name: Name) {
        self.name = name
        self.accidental = .natural
    }

    static let naturals: [Note] = Name.allCases.map(Note.init)
}

Private extension on Note

We also need to turn a note into a value, such as –1, 0, or 1, for our augment(previousNote:note:step:) function.

Let’s make a private extension so that it’s only reachable inside the file of notesIn(scale:). Because on its own, value doesn’t really mean anything on Note. Out of context, it can be anything, perhaps a frequency or a character. Since value is only a convenience for our own function, we’ll make it private. Alternatively, we could also make it a nested function inside notesIn(scale:)

private extension Note {
    var value: Int {
        switch accidental {
        case .natural: return 0
        case .flat: return -1
        case .sharp: return 1
        }
    }
}

Rewriting the parsing

One thing remains. Originally we parsed Note using its free initializer with a rawValue. Now that we have a struct Note instead of an enum, we lose the rawValue initializer. Let’s update the parser to support our new struct.

We’ll grab the iterator from the string using makeIterator(). This way we can pluck a character from it, one by one, by calling next(). Calling next() will return an optional Character each time.

First, we’ll try to convert the character into a Note.Name. Then we try to convert the second character (if any) to a Note.Accidental.

To support sharps and flats, we will convert # to .sharp and .flat. This allows people to pass strings to our program such as c# or Bb, which is easier to write.

extension Note {

    init?(string: String) {
        var iterator = string.makeIterator()
        // First we try to convert the first character to a note name.
        // We make it case insensitive by making it lowercased.
        guard let nameStr = iterator.next(),
              let name = Note.Name(rawValue: String(nameStr).lowercased()) else {
           return nil
        }

        // If we have a note name, we try to extract the accidental.
        if let accidentalStr = iterator.next() {

            let accidental: Note.Accidental
            switch accidentalStr {
            case "#": accidental = Accidental.sharp
            case "b": accidental = Accidental.flat
            default:
                return nil
            }

            self = Note(name: name, accidental: accidental)
        } else {
            self = Note(name: name)
        }
    }

}

Updating the CustomStringConvertible implementation

And finally, we’ll update the description to support CustomStringConvertible again.

extension Note: CustomStringConvertible {
    var description: String {
        name.rawValue.uppercased() + accidental.description
    }
}

Running our tests

All tests are now passing. Great!

A couple more things:

Let’s add C♯ and F♯ to our test-cases. They need these notes called a E♯ or B♯. Weird right? These notes do not appear on the piano, there is no black key after B or E. But, to fulfill our “one letter for each note scale”, it makes sense again. If we need to raise a B to fit the scale, we have a B♯, which is really a C. The same goes for the E♯, it’s a different name for an F.

The good news is, our code takes sharp B’s and E’s into account, it already works!

final class musicTests: XCTestCase {

    func testMajorScales() throws {
        let expectedPairs = [
            // We'll add a few more tests
            ("c#", "C♯ D♯ E♯ F♯ G♯ A♯ B♯"),
            ("f#", "F♯ G♯ A♯ B C♯ D♯ E♯"),
            // ... snip
    }

}

And finally, there are three scales we do not support. Namely A♯, D♯, and G♯. They require two more accidentals, namely a double-sharp and double-flat, which isn’t needed for now (or maybe ever). They are called theoretical scales and are impractical to read. So we’ll leave them out to keep our program simpler.

Implementing more features

Now that we have a proper major scale working. It will be much easier to add a lot of other methods that are useful for modeling music. Let’s go over a few.

Remember the major chord from the first article? It’s built from the first, third, and fifth note in a major scale.

For instance, the C major chord is built from C E G, and it’s made by combining the first, third, and fifth note from the C major scale.

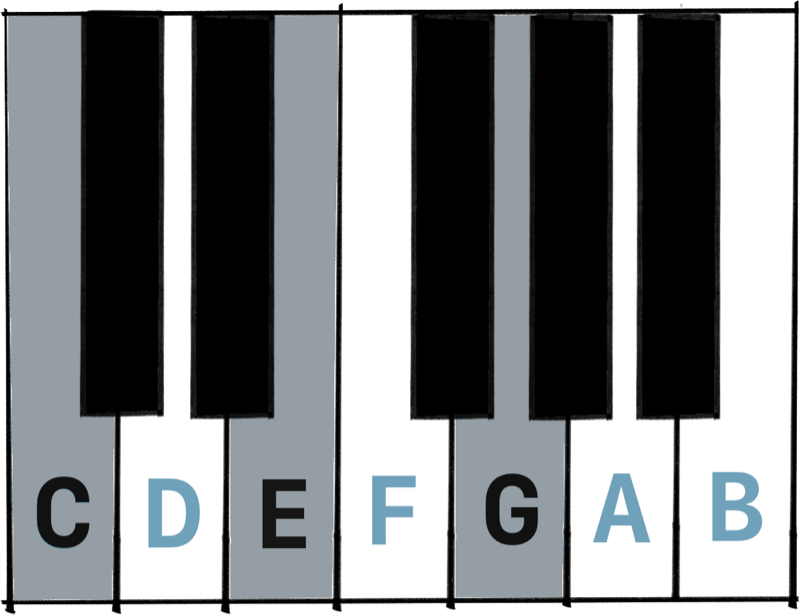
In programming, that would be index 0, 2, and 4 from a major scale. Let’s introduce the majorChordFor(note:) function.

func majorChordFor(note: Note) -> [Note] {
    let notes = notesIn(scale: note)
    return [notes[0], notes[2], notes[4]]
}

A minor chord is a major chord, with the 3rd note (the middle note) flattened. We can easily add that now by calling flatten() on the middle note. We’ll introduce a function called minorChordFor(note:).

func minorChordFor(note: Note) -> [Note] {
    let notes = notesIn(scale: note)
    return [notes[0], notes[2].flatten(), notes[4]]
}

Key signature

To give another demonstration of how useful it is that we modeled our notesIn(scale:) correctly. We can generate another thing called a key signature.

Basically, it’s the sharps or flats in a scale. For example, the G scale has one sharp in it, the F♯. So if you can remember “G… the key signature is only F♯”, then you know all the notes in the scale of G!

Now the thing is, with a key signature we need the sharps and flats to be ordered a certain way to memorize which scale has which sharps.

Naively, we could export the sharps alphabetically. For instance, for the scale of B we could print, A♯ C♯ D♯ F♯ G♯, but there’s a certain order to it.

The order is B E A D G C F for scales with sharps. And it’s reversed for scales that are flat, F C G D E A B. So we’ll add that, and we’re done. Again, notice how very little code we need.

func keySignature(note: Note) -> [Note] {
    let chars = "beadgcf"
    let order = note.accidental == .flat ? String(chars.reversed()) : chars
    return notesIn(scale: note).filter { note in note.accidental != .natural }.sorted { lhs, rhs in
        order.firstIndex(of: Character(lhs.name.rawValue))! > order.firstIndex(of: Character(rhs.name.rawValue))!
    }
}

These are just three examples, but now that our major scales are a solid foundation, we can start building a lot on top of it! (More to come later too.)

Updating run()

We can update run inside Music to support our new majorChordFor(note:) and minorChordFor(note:) functions and the new keySignature(note:) function.

First, let’s add a little Array extension to print notes in a nicer way, based on the code from the previous article.

extension Array {
    var description: String {
        self.map { String(describing: $0) }.joined(separator: " ")
    }
}

Then we’ll update Music’s run() method to support the new description property, and the three new functions. Notice how we’ll introduce two new flags, called minor and signature.

struct Music: ParsableCommand {

    // We add a new minor flag for minor chords
    @Flag(name: .shortAndLong, help: "Switch to minor (chords only).")
    var minor = false

    // We add a new signature flag for key signatures
    @Flag(name: .long, help: "")
    var signature = false

    // ... snip

    mutating func run() throws {
        // We match on a scale, signature, or Note.
        // flatMap is explained below.
        switch (scale, signature, note.flatMap(Note.init)) {
        case (true, _, let scale?):
            // Specific scale
            print(notesIn(scale: scale).description)
        case (true, _, nil):
            // Scale and no note.
            print("W W H W W W H")
        case (_, true, let note?):
            print(keySignature(note: note).description)
        case (_, _, let note?) where minor:
            print(minorChordFor(note: note).description)
        case (_, _, let note?):
            print(majorChordFor(note: note).description)
        default:
            // If we have no command at all, print the help-message.
            print(Music.helpMessage())
            break
        }
    }
}

Okay let’s try out our program!

Test-run

Let’s first make a release build, and move it so that we can run it from anywhere on the command line. For more detail about this, you can read the first article.

% swift build -c release
% sudo mv .build/release/music /usr/local/bin/

Then we’ll echo a bunch of notes so that they get printed out. Then we pipe | those notes to xargs, we use -n 1 to make it treat each input separately (so each note gets passed to music one by one). Then xargs will run a command (using sh -c), echoing the note and its scale using our music program.

% echo "a Bb b c c# d eb e f g" | xargs -n 1 sh -c 'echo Scale of "$0" is $(music --scale $0)'
Scale of a is A B C♯ D E F♯ G♯
Scale of Bb is B♭ C D E♭ F G A
Scale of b is B C♯ D♯ E F♯ G♯ A♯
Scale of c is C D E F G A B
Scale of c# is C♯ D♯ E♯ F♯ G♯ A♯ B♯
Scale of d is D E F♯ G A B C♯
Scale of eb is E♭ F G A♭ B♭ C D
Scale of e is E F♯ G♯ A B C♯ D♯
Scale of f is F G A B♭ C D E
Scale of g is G A B C D E F♯

If we omit --scale we get the major chords.

% echo "a Bb b c c# d eb e f g" | xargs -n 1 sh -c 'echo $0 major chord is $(music  $0)'
a major chord is A C♯ E
Bb major chord is B♭ D F
b major chord is B D♯ F♯
c major chord is C E G
c# major chord is C♯ E♯ G♯
d major chord is D F♯ A
eb major chord is E♭ G B♭
e major chord is E G♯ B
f major chord is F A C
g major chord is G B D

Minor chords will now work too by using the --minor flag.

% echo "a Bb b c c# d eb e f g" | xargs -n 1 sh -c 'echo $0 minor chord is $(music --minor $0)'
[1/1] Build complete!
a minor chord is A C E
Bb minor chord is B♭ D♭ F
b minor chord is B D F♯
c minor chord is C E♭ G
c# minor chord is C♯ E G♯
d minor chord is D F A
eb minor chord is E♭ G♭ B♭
e minor chord is E G B
f minor chord is F A♭ C
g minor chord is G B♭ D

And we can generate key signatures for flat and sharp major scales.

% echo "G D A E B F# C# F Bb Eb Ab Db Gb Cb" | xargs -n 1 sh -c 'echo Key signature of $0 is $(music --signature $0)'
Key signature of G is F♯
Key signature of D is F♯ C♯
Key signature of A is F♯ C♯ G♯
Key signature of E is F♯ C♯ G♯ D♯
Key signature of B is F♯ C♯ G♯ D♯ A♯
Key signature of F# is F♯ C♯ G♯ D♯ A♯ E♯
Key signature of C# is F♯ C♯ G♯ D♯ A♯ E♯ B♯
Key signature of F is B♭
Key signature of Bb is B♭ E♭
Key signature of Eb is B♭ E♭ A♭
Key signature of Ab is B♭ E♭ A♭ D♭
Key signature of Db is B♭ E♭ A♭ D♭ G♭
Key signature of Gb is B♭ E♭ A♭ D♭ G♭ C♭
Key signature of Cb is B♭ E♭ A♭ D♭ G♭ C♭ F♭

Let’s do recursion. We ask music for the C scale, and pass it back into music to turn all these notes into major chords.

% music --scale c | xargs -n 1 music
C E G
D F♯ A
E G♯ B
F A C
G B D
A C♯ E
B D♯ F♯

Conclusion

We covered a lot of ground! You’re doing a great job making it this far.

We now have a test-suite, support for flats, our Note type is more sophisticated, and most importantly: We can now build major scales!

This is good news. Because so much of music theory is built off of major scales, we can start doing the fun stuff, such as making music. We’ve already seen how easily we could add features with just a few lines of code!

Let’s look at where we are:

• The switch inside run() is fine, but it will become unwieldy if we keep adding features. We’d have to look at something called subcommands to make it more scalable.
• Also error handling is still missing. We are still only printing out error messages. This will not play nicely with other command line tools. And we’ve already starting to combine our program with others, as we’ve seen by passing values to our program.
• Our tool is becoming quite solid though, and will be a good basis for making the teaching aspect. So far just talking about notes gets a bit boring, I want to hear music! So maybe we should start thinking about adding sounds.

See you next time!